Engine Piston Optimization

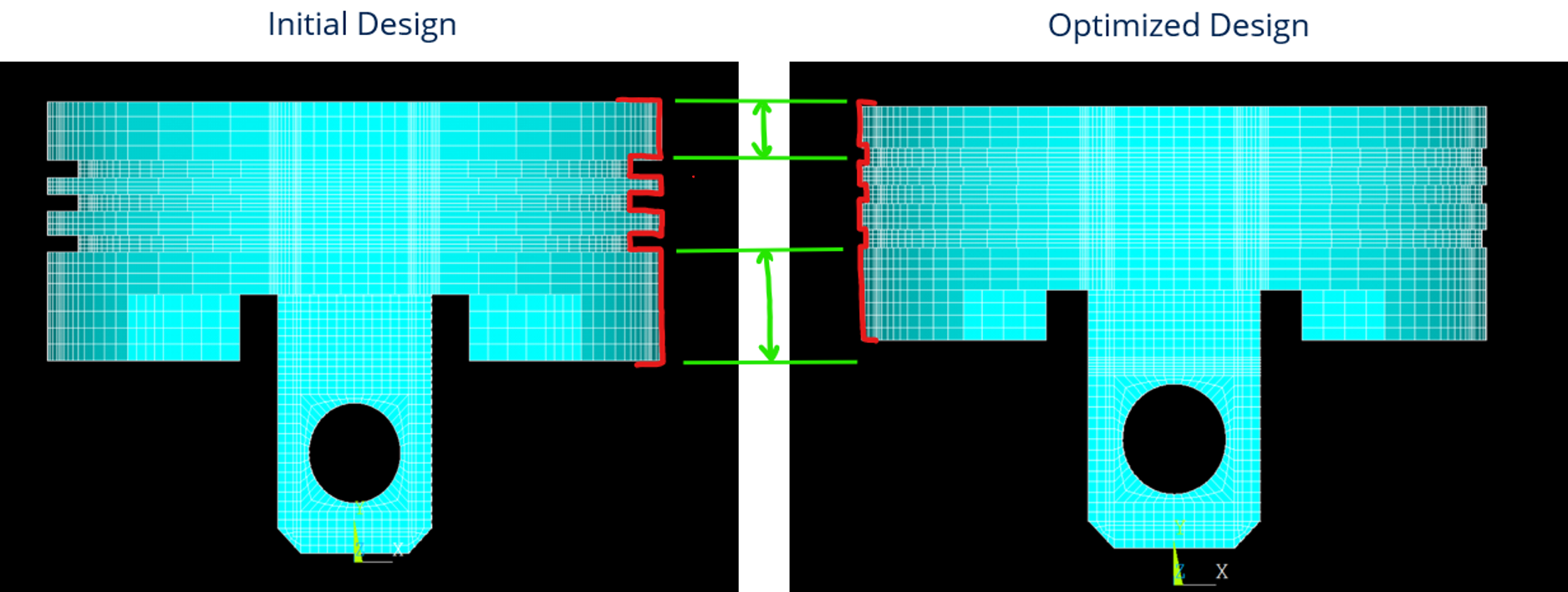
Project Overview

This project focused on the structural analysis and optimization of a high-performance race car engine piston. Using ANSYS Mechanical APDL, the goal was to reduce the piston's mass to improve engine response and efficiency while ensuring it could withstand the mechanical loads of racing engines.

The project involved bottom-up modeling, mesh generation, boundary condition application, and iterative optimization processes to determine the optimal design

Technical Challenge

Optimizing an engine piston requires balancing conflicting requirements:

• Weight Reduction: Minimizing reciprocating mass to increase RPM potential and reduce vibration.
• Structural Integrity: Withstanding high combustion pressures and inertial forces.

Design & Analysis

Modeling & Meshing

The piston was modeled using a bottom-up approach in ANSYS Mechanical APDL:

• Geometry Creation: Defined keypoints, lines, areas, and volumes to construct the piston geometry.
• Element Selection: Utilized appropriate 3D structural elements (e.g., SOLID185 or similar) for accurate stress prediction.
• Meshing Strategy: Implemented a hexahedral element mesh in high-stress regions (pin boss, crown) to ensure convergence and accuracy.

Finite Element Analysis (FEA)

Comprehensive simulations were conducted to validate the design:

• Static Structural Analysis: Applied distributed pressure load of 103,000 kPa to the piston crown.
• Boundary Conditions: Fixed constraints applied at the connecting rod and piston peg locations.
• Deflection Criteria: Ensured maximum downward deflection remained below 0.5 mm.
• Stress Evaluation: Analyzed Von Mises stresses to ensure they remained below the yield strength of 585 MPa.

Optimization Process

Design Optimization Strategy

To achieve the optimal strength-to-weight ratio, the project utilized the Conjugate Gradient Method, a first-order iterative optimization algorithm. The process was rigorous and designed to avoid local minima:

• Iterative Approach: The optimization was conducted over three separate trials, with each trial running for 40 iterations.
• Global Convergence: For each trial, the starting design values were varied. This multi-start strategy ensured that the final solution represented a global optimum rather than a local minimum.
• Parameterization: Key geometric features such as skirt thickness, crown thickness, and pin boss dimensions were defined as design variables.

Constraints & Objectives

• Objective Function: Minimize total volume (and thus mass).
• Constraints:
  • Maximum Von Mises stress < 585 MPa (Yield Strength of AISI 1045)
  • Maximum Deformation < 0.5 mm

Tools & Technologies

Key Achievements

• Design Optimization: Optimized piston geometry to minimize volume while satisfying strict deflection constraints.
• Stress Management: Verified that peak stresses (381 MPa) remained well within the yield strength of Steel AISI 1045 (585 MPa).
• Modeling Proficiency: Demonstrated advanced capability in ANSYS APDL scripting and analysis.

Results & Impact

The optimized piston design demonstrated a significant improvement over the initial baseline. By strategically removing material from low-stress areas, the final design achieved a lighter component without compromising safety margins.

Performance Metrics

• Volume Reduction: Successfully reduced the overall piston volume by 28%, fulfilling the primary project objective of minimizing mass.
• Material Selection: Switched from Aluminum 2618 to Steel AISI 1045 to meet deflection requirements (< 0.5 mm).
• Safety Factor: Achieved a safety factor of 1.53 against yield strength.
• Max Deformation: Limited to 0.40 mm, successfully meeting the < 0.5 mm design constraint.

This project served as an introduction to design optimization using finite element modelling.